In the world of electrical circuits, Kirchhoff’s Laws play a crucial role in understanding and analyzing complex circuit systems. These laws, also known as Kirchhoff’s Circuit Laws or KCL (Kirchhoff’s Current Law) and KVL (Kirchhoff’s Voltage Law), were developed by German physicist Gustav Kirchhoff in 1845.
Toc
Introduction to Kirchhoff’s Law

Gustav Kirchhoff, a notable German physicist, made significant contributions to the field of electrical engineering and physics. His most renowned work, Kirchhoff’s Laws, forms the bedrock of circuit analysis. These laws—Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL)—are indispensable tools for anyone serious about understanding and designing electrical circuits.
What is KCL?
Kirchhoff’s Current Law states that the total current entering a junction or node in an electrical circuit must equal the total current leaving the node. In essence, this law embodies the principle of conservation of charge. This means that no charge can be created or destroyed in an electrical circuit; it can only be transferred from one point to another.
The mathematical expression of KCL
The mathematical expression of KCL is as follows:
∑i = 0
This equation simply states that the sum of all currents entering a node must equal the sum of all currents leaving that same node. In other words, the algebraic sum of currents at a junction must be zero.
Explanation of KCL using the water pipe analogy
To understand KCL better, let’s use an analogy. Imagine a pipe carrying water that splits into two branches at a junction and then merges back into one pipe. According to the law of conservation of mass, the amount of water entering the junction must equal the amount of water leaving it.
In electrical circuits, currents behave in a similar manner to water flow in pipes. Just as we can’t have more or less water at any point along the pipe than what entered or left it, we can’t have more or less current at any node than what entered or left it. This is where Kirchhoff’s Current Law comes into play.
Practical applications of KCL
KCL has many practical applications, such as in circuit analysis and design. For instance, it is used to calculate unknown currents or verify the correctness of a circuit’s current values. It is also used in designing circuits to ensure that the currents are distributed correctly and do not exceed the maximum capacity of any components.
1. https://instaproapk.mobi/pii-protection-guide-securing-data-in-compliance-with-gdpr/
2. https://instaproapk.mobi/revolutionizing-hr-microsoft-viva-unveiled/
3. https://instaproapk.mobi/unlocking-small-business-potential-with-microsoft-access/
4. https://instaproapk.mobi/unleashing-the-power-nvidia-b100-for-gamers/
5. https://instaproapk.mobi/unlocking-creativity-with-adobe-cs6-a-guide-for-professionals/
The Importance of Kirchhoff’s Laws in Engineering
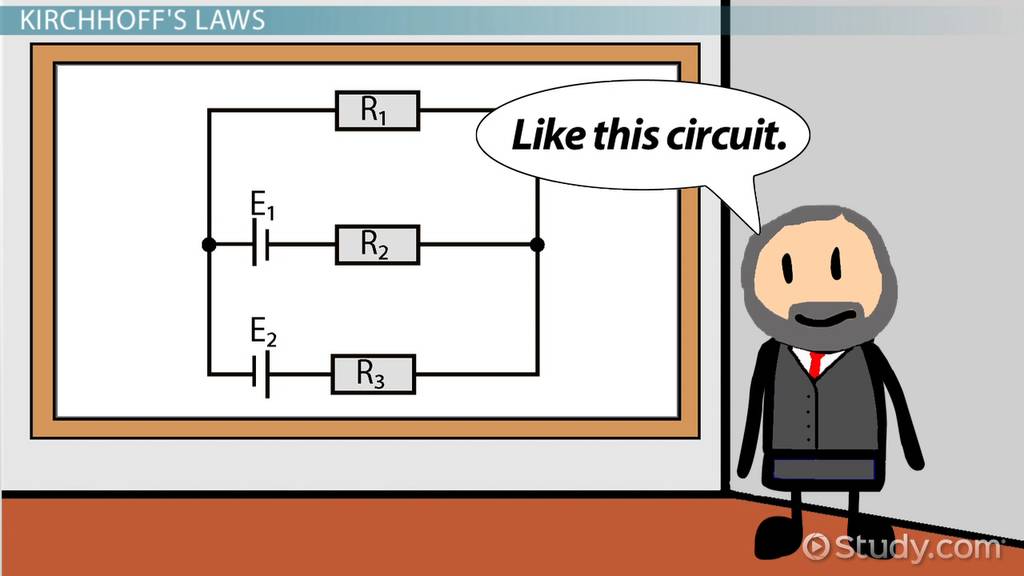
Fundamental for understanding circuit behaviour
Understanding Kirchhoff’s Laws is crucial for any electrical engineer or technician, as these principles provide the foundation for circuit analysis. By applying KCL and KVL, engineers can predict how currents and voltages will behave in various configurations. This knowledge allows for the troubleshooting of complex circuits, ensuring proper functionality and safety. Additionally, Kirchhoff’s Laws are integral in simulations and computational models, helping in the design of efficient power distribution systems and electronic devices. Without these laws, the exploration of modern electronics would be significantly hampered, highlighting their enduring relevance in contemporary engineering practices.
Ensuring Safe Operation
Kirchhoff’s Laws are essential for ensuring that circuits operate safely and within their specified limits. By applying KCL and KVL, engineers can predict how currents and voltages will behave in various components of the circuit, which is critical for preventing overloads and potential failures.
Facilitating the Use of Simulation Software
Modern circuit simulation software relies heavily on Kirchhoff’s Laws to model electrical behaviors accurately. Engineers utilize these laws to set up simulations that can predict how circuits will perform under different conditions, allowing for better design decisions and troubleshooting processes.
Supporting Complex Circuit Analysis
In more complex circuits, especially those including multiple components and branches, Kirchhoff’s Laws provide a systematic approach for solving for unknown currents and voltages. By using these laws in tandem with techniques such as mesh analysis and nodal analysis, engineers can deconstruct complex circuit designs into manageable calculations.
Interfacing with Other Electrical Principles
Kirchhoff’s Laws have significant relationships with other fundamental principles in electrical engineering, such as Ohm’s Law. By integrating KCL and KVL with these principles, a comprehensive understanding of circuit behavior can be achieved, leading to the development of more efficient and innovative electronic designs.
Misconceptions and Clarifications
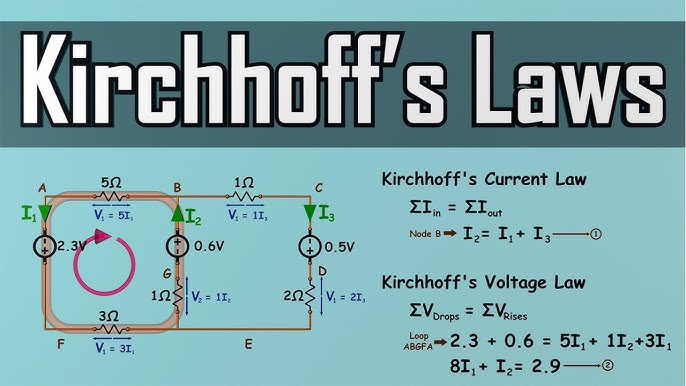
There are a few common misconceptions surrounding Kirchhoff’s Laws that need to be clarified.
KCL does not apply to series circuits
Some people mistakenly believe that KCL only applies to parallel circuits, but this is not true. KCL applies to all types of electrical circuits, including series and parallel arrangements. In series circuits, the same amount of current flows through each component, and according to KCL, the sum of these currents at any node must equal zero.
KVL does not apply to parallel circuits
Similarly, there is a misconception that KVL only applies to series circuits. However, just like KCL, KVL can be applied to all types of electrical circuits. In parallel circuits, the voltage drop across each branch may vary, but the sum of these drops must still equal the total voltage supplied by the source.
KVL does not mean that the sum of voltage drops around a closed loop must equal zero
While it is often stated as such for simplicity, this statement is technically incorrect. According to KVL, the algebraic sum of voltages around a closed loop must equal zero. This means that some voltages may add up positively while others may add up negatively, resulting in a total of zero. It is essential to understand this distinction for accurate circuit analysis.
Real-World Applications of KCL and KVL
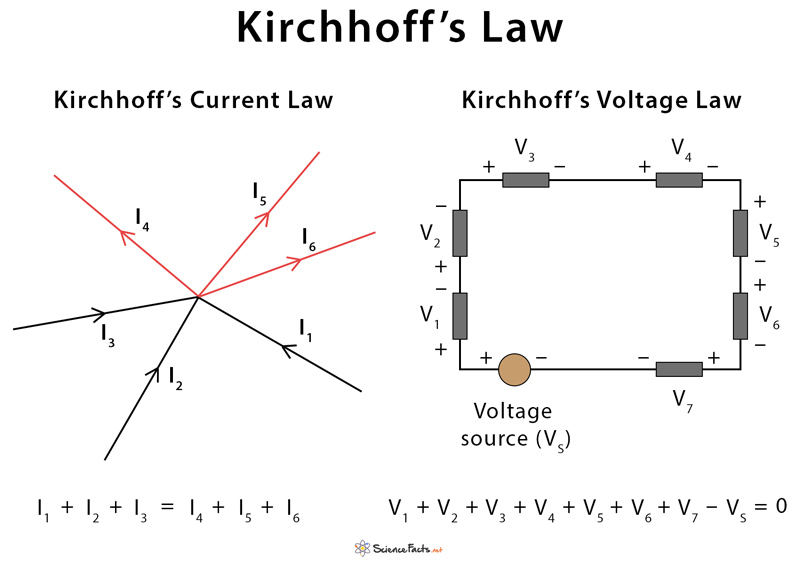
Kirchhoff’s Laws have numerous practical applications in various industries, including electronics, telecommunications, power systems, and more. Here are some real-world examples where these laws are applied:
Household Circuit Analysis
In household electrical systems, Kirchhoff’s Laws are applied to ensure that the current and voltages within the circuit remain balanced and safe. For instance, when assessing the total load on a circuit, engineers can use KCL to determine the total current flowing to various outlets and appliances. By ensuring that the sum of currents entering any junction equals the sum leaving, potential overloads can be identified and avoided. Additionally, KVL helps engineers check that the voltage drop across wiring, switches, and appliances does not exceed the total voltage supplied, thereby confirming that each component operates within its designated limits.
1. https://instaproapk.mobi/unlocking-creativity-with-adobe-cs6-a-guide-for-professionals/
2. https://instaproapk.mobi/revolutionizing-hr-microsoft-viva-unveiled/
3. https://instaproapk.mobi/pii-protection-guide-securing-data-in-compliance-with-gdpr/
4. https://instaproapk.mobi/unlocking-small-business-potential-with-microsoft-access/
5. https://instaproapk.mobi/unleashing-the-power-nvidia-b100-for-gamers/
Automotive Electrical Systems
In the automotive industry, Kirchhoff’s Laws are vital for designing and analyzing the complex electrical systems found in modern vehicles. By applying these laws, engineers can optimize the distribution of power to various components, such as lights, entertainment systems, and safety features. For example, KCL can be used to ensure that the current supplied to the headlights does not exceed what the circuit can handle, while KVL can verify that the voltage is adequate for the different systems under varying operational conditions, improving vehicle safety and performance.
Renewable Energy Systems
With the growing focus on sustainable energy, Kirchhoff’s Laws play a crucial role in the design and analysis of renewable energy systems, such as solar panels and wind turbines. By applying KCL, engineers can ensure that the output currents from multiple solar cells in a panel or from a series of wind turbines are properly managed and do not exceed the circuit limits. KVL is essential for determining the voltage across different components in the system, facilitating the effective integration of renewable sources into the existing power grid and ensuring efficient energy distribution.
Mobile Phone Charging Circuit
In mobile phone charging circuits, Kirchhoff’s Laws are applied to ensure that the current and voltage levels are appropriately matched to prevent damage to the device. Using KCL, engineers can verify that the current flowing through the charging circuit remains within safe limits, avoiding potential overheating or damage to the battery. Additionally, KVL aids in analyzing the voltage drops occurring across various components, such as resistors and diodes, ensuring that the overall voltage supplied by the charger meets the phone’s charging requirements. This careful balance is vital for the longevity and reliability of mobile devices.
Street Lighting Circuit Design
In street lighting systems, the application of Kirchhoff’s Laws helps in designing circuits that effectively manage power distribution and energy efficiency. KCL allows engineers to calculate the current flow required across multiple lighting fixtures, ensuring the combined load does not exceed the capacity of the power source. KVL is similarly important for evaluating voltage drops across lighting circuits, especially in long stretches where voltage loss might occur. By ensuring that each streetlight receives the appropriate voltage, KVL helps maintain consistency in illumination while optimizing energy usage, contributing to safer and more efficient urban environments.
Practical Examples and Analogies

To better understand and visualize the application of Kirchhoff’s Laws, here are a few practical examples and analogies that can be helpful:
Water Tank Analogy
Imagine a large water tank with multiple inlet pipes and outlet pipes. The level of water in the tank represents voltage, while the flow of water through each pipe represents current. Just as KCL states that the sum of currents entering any junction in an electrical circuit must equal the sum leaving, in this analogy, we can say that the rate at which water enters the tank must equal the rate at which it exits for the water level to remain constant.
Traffic Intersection Analogy
In a traffic intersection, cars from multiple roads merge and diverge, all while maintaining a continuous flow of traffic. Just like KVL states that the sum of voltage drops around a closed loop must equal zero, in this analogy, we can say that the number of cars entering an intersection must equal the number exiting for the traffic to remain steady.
Puzzle Pieces Analogy
Kirchhoff’s Laws can also be compared to a puzzle. Each individual piece represents a component in an electrical circuit, while the completed puzzle symbolizes a working circuit. Just as each piece is essential for completing the puzzle, each component plays a crucial role in ensuring proper current and voltage levels in an electrical circuit.
Mountain Hiking Analogy for KVL
When hiking up a mountain, imagine the elevation changes along the trail as representing the voltage changes in a circuit. Starting from the base, as you ascend, you gain elevation, which correlates with increasing voltage. However, the terrain may have various dips and rises, similar to voltage drops experienced at different components within a circuit. At any given point, the total change in elevation from the starting point to the summit must equal the net elevation change when descending back to the base. This mirrors Kirchhoff’s Voltage Law, which states that the sum of the voltage rises and drops around a closed loop in a circuit must be zero. Just as a hiker must account for every gain and loss in elevation to ensure a successful return, engineers must consider every voltage change in a circuit to ensure its proper operation.
Tea Party Analogy for Both Laws
Imagine a tea party where guests are filling their cups with tea from a communal teapot. The amount of tea poured into each cup represents the current flowing through each component in an electrical circuit. Kirchhoff’s Current Law (KCL) comes into play here, as the total amount of tea being poured from the teapot must equal the sum of tea consumed by all the cups—this reflects how the current entering a junction must equal the current leaving. Now, consider the temperature of the tea as an analogy for voltage. If the teapot’s tea starts at a certain temperature (representing initial voltage), each cup that receives tea might lose some heat due to various factors, such as the time it sits out or the material of the cup. This temperature loss corresponds to voltage drops across circuit components. According to Kirchhoff’s Voltage Law (KVL), the change in temperature from the teapot to all cups collectively must account for the initial temperature of the tea, akin to how the total voltage increase and decreases around a loop must equal zero. This analogy captures the essence of how currents and voltages interact within electrical circuits, emphasizing balance and conservation in both scenarios.
Conclusion

In summary, Kirchhoff’s Laws provide a foundational framework for understanding electrical circuits, allowing engineers and technicians to design systems that function efficiently and safely. By applying Kirchhoff’s Current Law and Voltage Law, professionals can make informed decisions regarding current distribution and voltage management, ensuring that each circuit operates within its specified limits. The use of analogies, such as the water tank, traffic intersection, puzzle pieces, mountain hiking, and tea party, aids in solidifying these concepts and making them more accessible. A thorough comprehension of these principles not only enhances circuit design but also contributes to the development of innovative technologies that rely on the intricate balance of electrical flow. As we advance our understanding of electronics, Kirchhoff’s Laws will continue to play an integral role in guiding the future of electrical engineering.





